Обмеження часу: 500 мс
Обмеження пам'яті: 64 Мбт
Ім'я вхідного файлу: a.in
Ім'я вихідного файлу: a.out
На уроці математики Степан вивчав системи числення, і на диво, він зрозумів новий матеріал. Особливо йому сподобалась трійкова система числення. Під час перерви між уроками він виписав усі числа від А до В у трійковій системі числення без ведучих нулів. Кожне число він записав на окремому листочку. Потім почав переставляти листочки так, щоб записані числа йшли у лексикографічному порядку. Пролунав дзвоник на урок, усі листочки Степан поспіхом зібрав, так і не завершивши свою роботу. Тепер Степана цікавить, яке число буде на першому місці, якщо отримані рядки розташувати у лексикографічному порядку. Числа А і В задаються в десятковій системі числення, відповідь також потрібно вивести у десятковій системі числення.
Наприклад, нехай А=2 і В=12. Тоді:| Числа в десятковій системі | Числа у трійковій системі | Трійкові числа лексографічному порядку |
| 2 3 4 5 6 7 8 9 10 11 12 | 2 10 11 12 20 21 22 100 101 102 110 | 10 100 101 102 11 110 12 2 20 21 22 |
Вхідні дані:
Перший рядок вхідного файлу містить два натуральних числа А і В (1≤A≤B≤1015).
Вихідні дані: Формат вихідних даних. Виведіть одне число – відповідь на задачу.
Приклад вхідних та вихідних даних.
| Приклад вхідних даних: | Приклад вихідних даних: |
| 2 12 | 3 |
Задача B - Чаювання дівчат
Обмеження часу: 1 с
Обмеження пам'яті: 64 Мбт
Ім'я вхідного файлу: b.in
Ім'я вихідного файлу: b.out
Перед святами Степан з братом Мишком вирішили влаштувати однокласницям чаювання і заразили своєю ідеєю ще K–2 своїх друзів. Вони зібрались разом і вибрали в одному досить відомому супермаркеті P тістечок. Настала черга розраховуватися за них. В магазині є N працюючих кас, занумерованих числами від 1 до N. Про i-у касу відомо, що касиру потрібно Ai одиниць часу на опрацювання одного товару і Bi одиниць часу для того, щоб розрахуватись із покупцем. Обійшовши усі каси, школярі порахували, що на обслуговування покупців, які вже стоять в i-ю касу, піде Ti одиниць часу. Тепер Степан і Мишко задались питанням, в які каси потрібно встати їм і їх друзям (в кожну із вибраних кас повинен стояти хоча б один із них, і кожен із них може стояти не більш, чим в одну касу, тому сумарно вони можуть стоять не більше чим в K кас) і скільки тістечок кожен має взяти, щоб останній із них вийшов із магазину як можна раніше. Дехто із хлопців можуть в касу не стояти, а, віддавши усі тістечка іншим, вийти через спеціальний вихід для тих, хто нічого не купив. Напишіть програму, яка визначає цей мінімальний час.
Вхідні дані: У першому рядку записано одне число N - кількість кас в супермаркеті (1≤N≤100000). В наступних N рядках записано по три числа Ai, Bi, Ti (0≤Ai, Bi, Ti≤100000). В останньому рядку записані два числа – K і P – число школярів і покупок у них відповідно (0≤P≤100000, 2≤K≤100000). Усі числа у вхідному файлі цілі.
Вихідні дані: Виведіть мінімальний час виходу останнього школяра із магазина.
Коментар прикладу 1:Саме вигідніше всього стати в обидві каси і купити там по одному тістечку.
Коментар прикладу 2:
Вигідніше всього одному із школярів стати з усіма тістечками в першу касу, а іншим вийти без покупок.
Приклад вхідних та вихідних даних.
| Приклад вхідних даних: | Приклад вихідних даних: |
| 2 100 10 40 10 100 50 2 2 | 160 |
| 3 1 2 0 5 2 1 2 10 1 3 5 | 7 |
Задача C - Трикутники
Обмеження часу: 2 с
Обмеження пам'яті: 64 Мбт
Ім'я вхідного файлу: c.in
Ім'я вихідного файлу: c.out
Геометрія – один з нелюбимих предметів Степана. Та ще і вчителька математики Л.І. незлюбила Степана (по крайній мірі він так думає) і завдання для нього підбирає не аби які, а підвищеної складності. От і сьогодні Степан сидить над задачею і нічого у нього не виходить. Думав написати програму розв’язку, та щось також не пішло. Тому просить у вас допомоги. Дано K точок з додатними цілими координатами. Також задано М трикутників, кожний з яких має початок координат, як одну з вершин та інші дві вершини з невід’ємними цілими координатами. Вам потрібно для кожного трикутника визначити, чи має він хоча б одну з даних K точок всередині. Гарантується, що жодна з заданих K точок не лежить на стороні жодного з заданих трикутників.
Вхідні дані: Перший рядок вхідного файлу містить числа K та M. Наступні K рядків будуть містити по 2 цілих додатних числа x та y розділених одним пробілом, що задають координати кожної точки. Наступні M рядків містять 4 невід’ємних цілих числа розділених одним пробілом, x1, y1, x2, y2, що задають 2 вершини кожного трикутника, окрім вершини, що є початком координат.
Вихідні дані: Вихідний файл повинен містити рівно M рядків. k-ий рядок повинен містити символ Y, якщо k-ий трикутник (в порядку, заданому у вхідному файлі), містить хоча б одну з K точок всередині, та N в іншому випадку.
Обмеження: 1≤K, M≤100000
1≤ кожна координата K точок ≤109
0≤ кожна координата вершин трикутників ≤109
Трикутники не вироджені (їхні площі відмінні від нуля).
1≤ кожна координата K точок ≤109
0≤ кожна координата вершин трикутників ≤109
Трикутники не вироджені (їхні площі відмінні від нуля).
В 50% тестів, всі трикутники мають вершини з координатам x1=0 та y2=0. Тобто, одна з сторін трикутника лежить на вісі абсцис, а інша на вісі ординат.
Пояснення прикладу 1:
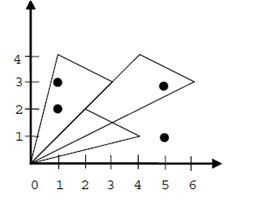
Пояснення прикладу 2:
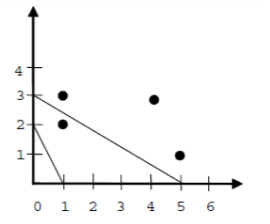
Приклад вхідних та вихідних даних.
Пояснення прикладу 1:

Пояснення прикладу 2:

Приклад вхідних та вихідних даних.
| Приклад вхідних даних: | Приклад вихідних даних: |
| 4 3 1 2 1 3 5 1 5 3 1 4 3 3 2 2 4 1 4 4 6 3 | Y N Y |
| 4 2 1 2 1 3 5 1 4 3 0 2 1 0 0 3 5 0 | N Y |