Задача А
Час на роботу програми відводився із великим запасом і це давало змогу перебирати всі числа із проміжків по два рази – для підрахунку та виведення простих чисел. Для визначення простоти числа k треба шукати дільники лише від 2 до - тоді програма вільно вкладається у визначений час.
Приклад функції для перевірки чисел на простоту (python).
def prost(k): // заголовок функції
if k == 1: return False // якщо 1, то повертаємо Хибно
for i in range(2,int(k**0.5)+1): // і пробігає від 2 до
if k % i == 0: // якщо і – дільник, то повертаємо Хибно
return False
return True // якщо ми тут, то k-просте і повертаємо Істино
Думаю, не важко написати щось подібне на іншій мові програмування.
Задача В
Ця задача просто пишеться на Python і вимагає клопіткої роботи на інших мовах програмування.
Авторська програма:
fo = open("numbers.out","w",1)
maxx = -10**1000
minn = 10**1000
for line in open("numbers.in","r",1):
if int(line)>maxx: maxx = int(line)
if int(line)<minn: minn = int(line)
fo.write(str(minn)+"\n")
fo.write(str(maxx)+"\n")
fo.close()
Програма є зрозумілою і без коментарів.
Рекомендації для створення програми на інших мовах програмування:
1. Числа зручно зчитувати у рядкову величину, для Паскаль слід використовувати тип ansistring.
2. Провести «нормалізацію» числа – видалити знак «-» та не значущі нулі. Для збереження знаку числа можна використати «прапорець». Напевне, вистачить три «прапорці» - для мінімального, для максимального і для активного числа (з цим числом ми працюємо)
3. Активне число порівнюємо окремо з мінімальним і максимальним.
4. При порівнянні зважаємо спочатку на знак числа, потім на довжину числа і якщо висновок не зроблено, то перевіряємо числа порозрядно.
Задача С
Ця задача «три в одному» - задача 1: знайти точки перетину прямих (кожна пряма перетинається із всіма іншими); задача 2: побудувати випуклу оболонку для точок перетину прямих; задача 3: знайти площу випуклого многокутника.
На всіх етапах ми працюємо із різними математичними формулами і тому накопичуються похибки обчислень, які залежать від багатьох факторів: методів обчислення, вибраних компіляторів, типів змінних та ін. Тому було прийняте рішення виводити довільну кількість знаків, а зараховувалися відповіді, які відрізнялися від еталону не більше 0,01.
Задача 1. Точка перетину двох прямих.
Нехай прямі задані своїми рівняннями:
A1x + B1y + C1 = 0, A2x + B2y + C2 = 0.
Для визначення координати точки перетину треба розв’язати систему цих рівнянь. Використовуючи формули Крамера ми отримаємо:
x = dx / d,
y = dy / d.
Де
d = A1 * B2 – B1 * A2,
dx = -C1 * B2 + B1 * C2
dy = -A1 * C2 + C1 * A2.
Якщо d=0, то прямі паралельні (у нас такого не буде).
Задача 2. Випуклий многокутник.
Многокутник називається випуклим, якщо всі його вершини лежать по одну сторону будь якої його сторони.
Щоб з’ясувати чи лежать дві точки по одну сторону прямої Ax + By + C = 0, треба користуватися таким правилом: дві точки лежать по різні сторони від даної прямої тоді і тільки тоді, коли при підстановці координат цих точок в рівняння прямої ми отримаємо відповіді протилежних знаків.
Побудова мінімальної випуклої оболонки.
1. Знаходимо саму ліву точку множини і приймаємо її за першу вершину оболонки.
2. За наступну вершину беремо ту точку, для якої відрізок, що має кінці на попередній вершині та даній точці, видно з останньої вершини під максимальним кутом. (Для першої вершини оболонки в якості попередньої треба взяти точку з координатами (x+1,y), де (x,y) – координати першої вершини).
3. Пункт 2 повторюємо до тих пір, поки чергова знайдена вершина не співпаде з першою.
Є інші алгоритми знаходження випуклої оболонки описані у літературі з алгоритмізації та програмування.
Задача 3.
Площа довільного многокутника з вершинами в (x1,y1),(x2,y2),…(xn,yn) визначається за формулою: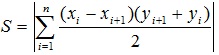
При цьому xn+1=x1, yn+1=y1
Час на роботу програми відводився із великим запасом і це давало змогу перебирати всі числа із проміжків по два рази – для підрахунку та виведення простих чисел. Для визначення простоти числа k треба шукати дільники лише від 2 до - тоді програма вільно вкладається у визначений час.
Приклад функції для перевірки чисел на простоту (python).
def prost(k): // заголовок функції
if k == 1: return False // якщо 1, то повертаємо Хибно
for i in range(2,int(k**0.5)+1): // і пробігає від 2 до
if k % i == 0: // якщо і – дільник, то повертаємо Хибно
return False
return True // якщо ми тут, то k-просте і повертаємо Істино
Думаю, не важко написати щось подібне на іншій мові програмування.
Задача В
Ця задача просто пишеться на Python і вимагає клопіткої роботи на інших мовах програмування.
Авторська програма:
fo = open("numbers.out","w",1)
maxx = -10**1000
minn = 10**1000
for line in open("numbers.in","r",1):
if int(line)>maxx: maxx = int(line)
if int(line)<minn: minn = int(line)
fo.write(str(minn)+"\n")
fo.write(str(maxx)+"\n")
fo.close()
Програма є зрозумілою і без коментарів.
Рекомендації для створення програми на інших мовах програмування:
1. Числа зручно зчитувати у рядкову величину, для Паскаль слід використовувати тип ansistring.
2. Провести «нормалізацію» числа – видалити знак «-» та не значущі нулі. Для збереження знаку числа можна використати «прапорець». Напевне, вистачить три «прапорці» - для мінімального, для максимального і для активного числа (з цим числом ми працюємо)
3. Активне число порівнюємо окремо з мінімальним і максимальним.
4. При порівнянні зважаємо спочатку на знак числа, потім на довжину числа і якщо висновок не зроблено, то перевіряємо числа порозрядно.
Задача С
Ця задача «три в одному» - задача 1: знайти точки перетину прямих (кожна пряма перетинається із всіма іншими); задача 2: побудувати випуклу оболонку для точок перетину прямих; задача 3: знайти площу випуклого многокутника.
На всіх етапах ми працюємо із різними математичними формулами і тому накопичуються похибки обчислень, які залежать від багатьох факторів: методів обчислення, вибраних компіляторів, типів змінних та ін. Тому було прийняте рішення виводити довільну кількість знаків, а зараховувалися відповіді, які відрізнялися від еталону не більше 0,01.
Задача 1. Точка перетину двох прямих.
Нехай прямі задані своїми рівняннями:
A1x + B1y + C1 = 0, A2x + B2y + C2 = 0.
Для визначення координати точки перетину треба розв’язати систему цих рівнянь. Використовуючи формули Крамера ми отримаємо:
x = dx / d,
y = dy / d.
Де
d = A1 * B2 – B1 * A2,
dx = -C1 * B2 + B1 * C2
dy = -A1 * C2 + C1 * A2.
Якщо d=0, то прямі паралельні (у нас такого не буде).
Задача 2. Випуклий многокутник.
Многокутник називається випуклим, якщо всі його вершини лежать по одну сторону будь якої його сторони.
Щоб з’ясувати чи лежать дві точки по одну сторону прямої Ax + By + C = 0, треба користуватися таким правилом: дві точки лежать по різні сторони від даної прямої тоді і тільки тоді, коли при підстановці координат цих точок в рівняння прямої ми отримаємо відповіді протилежних знаків.
Побудова мінімальної випуклої оболонки.
1. Знаходимо саму ліву точку множини і приймаємо її за першу вершину оболонки.
2. За наступну вершину беремо ту точку, для якої відрізок, що має кінці на попередній вершині та даній точці, видно з останньої вершини під максимальним кутом. (Для першої вершини оболонки в якості попередньої треба взяти точку з координатами (x+1,y), де (x,y) – координати першої вершини).
3. Пункт 2 повторюємо до тих пір, поки чергова знайдена вершина не співпаде з першою.
Є інші алгоритми знаходження випуклої оболонки описані у літературі з алгоритмізації та програмування.
Задача 3.
Площа довільного многокутника з вершинами в (x1,y1),(x2,y2),…(xn,yn) визначається за формулою:
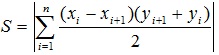
При цьому xn+1=x1, yn+1=y1